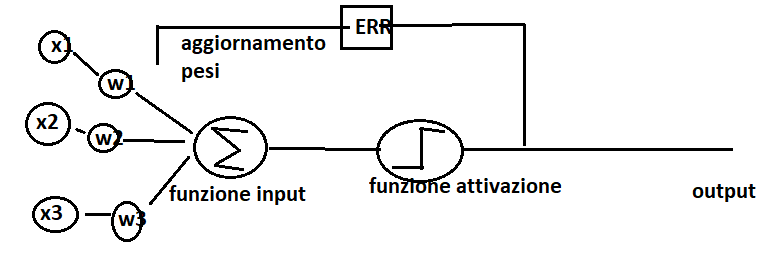
Immaginiamo di modellare un neurone artificiale come un elaboratore che può avere segnali in input e segnali di output. Il segnale entra attraverso i dendriti della cellula ed attraverso l’assone arriva fino ai terminali. Quando il segnale in input supera una determinata soglia allora si attiva il neurone e l’output è positivo. Al contrario l’output rimane negativo.
Il problema descritto sopra può essere rappresentato come un compito di classificazione binaria (+1; -1). I dati in ingresso entrano dentro l’elaboratore, che modelliamo con una funzione di attivazione Θ(z) e dove z è l’input della rete.
La funzione di attivazione che vogliamo utilizzare è a passo unitario, ovvero:
Avendo un serie di campioni che entrano nell’elaboratore (dataset) possiamo descrivere l’input in forma vettoriale:
z=w1 x1 + w2 x2 + w3 x3 + w4 x4 +…+ wm xm
wn-> pesi della funzione
x-> rappresentano le caratteristiche del campione e sono espresse in forma vettoriale
In linea teorica noi dovremmo trovare un algoritmo che dato in ingresso un serie di dati, classifica ogni campione sulla base delle caratteristiche. Il modello che intendiamo analizzare è un classificatore binario, quindi, preso in ingresso una serie di dati, in base alle caratteristiche, produce una classificazione binaria (1, -1).
Una volta “addestrato” il modello per produrre la classificazione binaria allora, ad ogni nuovo campione in ingresso, siamo in grado di predirne la classificazione (1, -1).
La classificazione è il risultato della funzione di attivazione che preso in ingresso l’input della rete si attiva soltanto se superiamo una determinata soglia θ:
Θ(z)=1 if z>=θ
Θ(z)=-1 altrimenti
oppure, in forma più compatta, portando la soglia alla sinistra dell’equazione:
Θ(z)=1 if z>=θ –> z-θ>=0
z-θ=w1 x1 + w2 x2 + w3 x3 + w4 x4 +…+ wm xm -> z= θ + w1 x1 + w2 x2 + w3 x3 + w4 x4 +…+ wm xm
L’ algoritmo perceptron che emula il neurone si comporterà come segue:
- inizializzazione dei pesi a 0 o numeri casuali piccoli
- calcolo del valore output y–: etichetta della classe prevista
- aggiornamento dei pesi: wj = wj + Δwj, dove Δwj=η(y(i) – y-(i))x(i)j
Dalle formule è evidente che se una predizione risulta errata allora l’aggiornamento del peso avviene in modo proporzionale nella direzione della classe target corretta.
Ad esempio, se abbiamo un campione x(i)j = 2 e l’abbiamo predetto nella classe errata y-(i)= -1 ed il tasso di apprendimento η=1, allora, l’aggiornamento del peso risulta essere:
Δwj=η(y(i) – y-(i))x(i)j = Δwj=1(1 – -1)2 = 4, l’algoritmo aggiorna i pesi in maniera proporzionale verso la classe corretta.
In conclusione, il perceptron, è un algoritmo di classificazione binaria in grado di predire una determinata classe attraverso le caratteristiche del campione.
